python算法实现
算法时间复杂度主要看:一般情况和最坏情况
二分查找
def binary_search(li, val):
"""
:param li:传入列表
:param val: 需要查找的值
:return: val
"""
left = 0 # 指针left:起始最小长度为0
right = len(li) - 1 # 指针right:最大长度为列表长度-1
while left <= right: # 指针left<=right时说明列表有1~2个值
mid = (left + right) // 2 # 找到中间值
if li[mid] > val: # 二分出来的值与待查找的值进行比较
right = mid - 1 # right指针移动到mid处-1的位置,即mid左边一位
elif li[mid] < val:
left = mid + 1 # left指针移动到mid处+1的位置,即mid右边一位
else: # val=mid
return mid #拿到找到的值
else: # 指针left>right
时
return None # 列表没有需要查找的值
lowb三人组(时间复杂度O(n^2))
冒泡排序
原理:冒泡排序,长度为n的列表,走n-1趟
每走一趟,把无序区最大的数放在最后,即冒泡,并把无序区的其他比较大的数,稍微往上移了一些
指针走到n-1停下,因为n为冒泡的数,之后重新回到无序区0的位置
走i趟,则指针在n-1-i(-1:指针每次都少走一位,因为n为要冒泡的值;-i:第i趟,就已经有i个冒泡的值)
def bubble_sort_plus(li):
for i in range(len(li) - 1):
# i表示第i趟 有序区有i个数
exchange = False # 标识符为False
for j in range(len(li) - i - 1): # 循环无序区
if li[j] > li[j + 1]: # 如果指针j大于j+1,则需要移动位置
li[j], li[j + 1] = li[j + 1], li[j] # 当前位置j替换成j+1,j+1替换成j
exchange = True # 如果有交换位置则改为True
if not exchange: # 如果走完一趟,依然为False
return # 则说明这一趟不改变顺序,为有序,减少循环次数
执行结果: li = [2,5,4,8,7,6,9,1,3]
[2, 4, 5, 7, 6, 8, 1, 3, 9]
[2, 4, 5, 6, 7, 1, 3, 8, 9]
[2, 4, 5, 6, 1, 3, 7, 8, 9]
[2, 4, 5, 1, 3, 6, 7, 8, 9]
[2, 4, 1, 3, 5, 6, 7, 8, 9]
[2, 1, 3, 4, 5, 6, 7, 8, 9]
[1, 2, 3, 4, 5, 6, 7, 8, 9]
总结:冒泡排序时间复杂度O(n**2)速度太慢
如果冒泡执行一趟没有进行交换,则已经是排好序的列表,直接结束算法
选择排序
原理:选择排序:遍历列表,找到最小的数,放在首位
def select_sort(li):
for i in range(len(li)-1):
# 第i趟:有序区li[0:i] 无序区li[i:n],第一趟就位i=0的索引值
min_loc = i # 当前循环无序区最小的值,第一次为索引0
for j in range(i+1, len(li)): # 循环无序区
if li[min_loc] > li[j]: # 当前有序区的最大值对比无序区的值
min_loc = j # 下标交换
li[min_loc], li[i] = li[i], li[min_loc] # 位置进行交换,相当于li[j]与li[i]进行交换
print(li)
执行结果:li = [2,5,4,8,7,6,9,1,3]
[1, 5, 4, 8, 7, 6, 9, 2, 3]
[1, 2, 4, 8, 7, 6, 9, 5, 3]
[1, 2, 3, 8, 7, 6, 9, 5, 4]
[1, 2, 3, 4, 7, 6, 9, 5, 8]
[1, 2, 3, 4, 5, 6, 9, 7, 8]
[1, 2, 3, 4, 5, 6, 9, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 9, 8]
[1, 2, 3, 4, 5, 6, 7, 8, 9]
插入排序
原理:扑克牌排序
每次从无序区选择一个元素插入有序区(此方法为相对有序),直至无序区变空
一共有n张牌,开始有一张,一共模n-1次牌
def insert_sort(li):
for i in range(1, len(li)): # i既表示趟数,也表示摸到的牌的下标
j = i - 1 # j指手里的最后一张牌的下标,第一趟只有一张牌,即列表第一个值,下标为0
tmp = li[i] # 在无序区新拿到的值
print(tmp)
print(li[j])
while j >= 0 and li[j] > tmp: # 当手上的牌还有牌大于新的牌 and 当手上最右边的牌大于新摸到的牌tmp
# while循环的作用:找插入位置
li[j + 1] = li[j] # j指针的位置(手上最右边的牌)向右移一个单位
j -= 1 # 指针向左移一个单位,找手上从右往左第二个值,再循环进行比较
li[j + 1] = tmp # 大于新摸到的牌,全部向右移一个单位,下标j+1(新摸得牌的下标)处为新的数
print(li)
执行结果:li = [2,5,4,8,7,6,9,1,3]
[2, 5, 4, 8, 7, 6, 9, 1, 3]
[2, 4, 5, 8, 7, 6, 9, 1, 3]
[2, 4, 5, 8, 7, 6, 9, 1, 3]
[2, 4, 5, 7, 8, 6, 9, 1, 3]
[2, 4, 5, 6, 7, 8, 9, 1, 3]
[2, 4, 5, 6, 7, 8, 9, 1, 3]
[1, 2, 4, 5, 6, 7, 8, 9, 3]
[1, 2, 3, 4, 5, 6, 7, 8, 9]
一般电脑一秒钟运算10^7=一千万次,可以估算时间复杂度的实际时间
牛逼三人组
快速排序
原理:取一个元素P(第一个元素),使元素P归位(让p元素,左边比p小,右边比p大)
列表被p分成两部分,左边比p小,右边比p大
递归完成排序
注意:不能给递归函数加装饰器,会导致执行n次装饰器内容,则可对递归函数进行封装优化
def _quick_sort(li, left, right):
"""
快排
:param li: 需要排序的列表
:param left: 左边第一个下标0
:param right: 右边第一个下标len(li)-1
:return:
"""
if left < right: # left=right一个元素,left>right没有元素
mid = partition(li, left, right) # 调用函数返回归位元素下标
# 递归归位元素两侧
_quick_sort(li, left, mid - 1) # mid左边
_quick_sort(li, mid + 1, right) # mid右边
def partition(li, left, right):
########最坏情况优化方案#########
# 原本是找第一个数,li[left]进行从右往左的查找
i = random.randint(left, right) # 随机从列表中找一个数的下标
li[left], li[i] = li[i], li[left] # 让第一个数li[left]交换成随机选择的数li[i]
###############################
tmp = li[left] # 拿到左边第一个元素
while left < right: # 当游标left<right时一直循环,left=right找到mid
# 从右边找比tmp小的数,因为左边有空位(把tmp拿出来),比tmp小的数放在左边
while left < right and li[right] >= tmp: # 当右边的数一直大于tmp时,则会一直遍历找到比tmp小的值停止
#需要添加left<right防止右边的数一直大于左边的数而无法退出循环,当left=right时说明右边全部值大于tmp
right -= 1 # 往左走一步
li[left] = li[right] # 找到右边的值小于tmp的,填写到左边空位
# 从左边找比tmp大的数,因为右边有空位,比tmp大的数放到右边
while left < right and li[left] <= tmp: # 从左边找比tmp大的值
left += 1
li[right] = li[left] # 把左边的值写到右边的空位上
li[left] = tmp # 把tmp归位,即跳出大的循环,left=right使左边小于tmp,右边大于tmp
return left # 返回mid值,left=right=mid
时间复杂度:O(nlogn) = 有logn层(深度),每层时间复杂度为n(从左到右,从右到左遍历)
快速排序问题:
最坏情况:倒序排序 9 8 7 6 5 4 3 2 1 复杂度为n^2
递归:设置递归深度
解决的方式是手工设置递归调用深度,方式为:
import sys
sys.setrecursionlimit(1000000) #例如这里设置为一百万
堆排序
学前必备知识
树
1.树是一种数据结构,比如:目录结构
2.树是一种可以递归定义的数据结构
3.树是由n个节点组成的集合:
* 如果n=0,那这是一颗空树;
* 如果n>0,那存在1个节点作为树的根节点,其他节点可以分为m个集合,每个集合本身又是一颗树(子树)
4.一些概念
* 根节点、叶子节点(不能分叉的节点)
* 树的深度(高度),看节点数
* 树的度:是整个树里节点度数(节点的度就是看分了几个叉)最大的度
* 孩子的节点/父节点
* 子树
二叉树
1.二叉树:就是度不超过2的数,即每个节点最多分2个叉
2.每个节点最多有两个孩子节点,因为度不超过2
3.两个孩子节点被区分为左孩子节点和右孩子节点
4.满二叉树:一个二叉树,如果每一个层的节点数都达到最大值,即度数都为2,则这个二叉树称为满二叉树
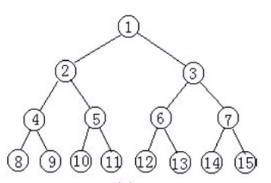
5.完全二叉树:叶子节点只能出现在最下层和次下层,并且最下面一层的节点都集中在该层最左边的若干位置的二叉树
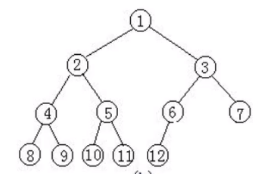
6.二叉树的存储方式
* 链式存储方式
* 顺序存储方式(堆排序使用顺序存储,即列表)

堆:一种特殊的完全二叉树结构
* 大根堆:一棵完全二叉树,满足任一节点都比其孩子节点大
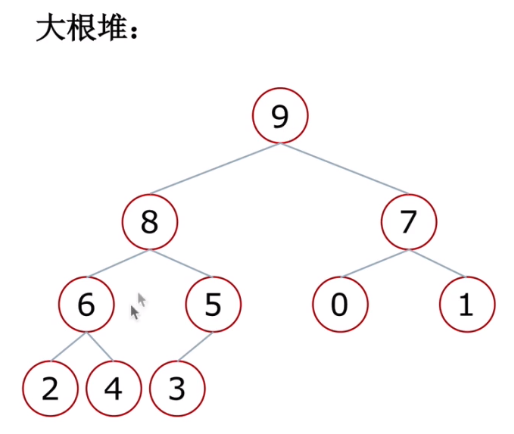
* 小根堆:一棵完全二叉树,满足任一节点都比其孩子节点小
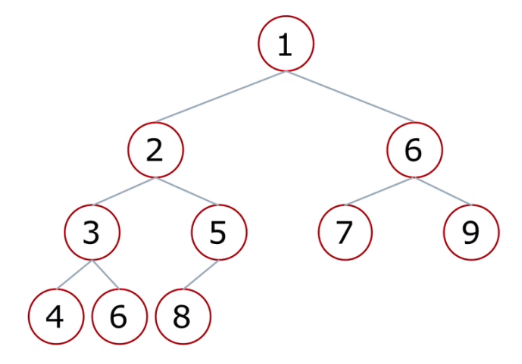
堆的向下调整:当根节点的左右子树都是堆时,可以通过一次向下的调整来将其变换成一个堆
堆排序的过程:
1.建立一个堆(从最后一个非叶子结点进行排序,慢慢扩大范围,直到整个堆)
2.得到堆顶元素,为最大元素
3.去掉堆顶,将堆最后一个元素(最后一个非叶子结点)放到堆顶,此时可以通过调整重新使堆有序
4.堆顶元素为第二大元素
5.重复步骤3,直到堆变空
def sift(li, low, high):
"""
向下调整函数的实现
:param li: 列表
:param low: 堆的根节点位置
:param high: 堆的最后一个元素的位置
:return:
"""
i = low # i最开始指向根节点
j = 2 * i + 1 # j开始指向左孩子
tmp = li[low] # 把堆顶保存起来,以便向下调整
while j <= high: # 只要j位置有数,即小于或等于最后一个元素
if j + 1 <= high and li[j + 1] > li[j]: # 如果有右孩子且右孩子>左孩子
# 用于判断j指向左右哪边
j = j + 1 # j指向右孩子
if li[j] > tmp: # 比堆顶大
li[i] = li[j] # 新的堆顶为li[j]
# 往下看一层,i和j向下移一层
i = j # i向下移到j
j = 2 * i + 1 # j向下移到i的左孩子节点
else: # tmp更大,则把tmp放在i位置
li[i] = tmp # 把tmp放在某一个领导(非叶子结点)位置上
break
else:
li[i] = tmp # 如果j>high,把tmp放在叶子节点上
# sift时间复杂度为logn,因为最多走树的高度logn,不是走左边就是走右边
"""
子节点---(n-1)//2--->父节点
列表最后一个元素索引len(n)-1,其中len(n)=n
"""
def heap_sort(li):
"""
建立一个堆
(从最后一个非叶子结点进行排序,慢慢扩大范围,直到整个堆)
:param li:
:return:
"""
n = len(li)
# 最后一个非叶子结点(n-1-1)//2
for i in range((n - 2) // 2, -1, -1): # 参数1:range左范围,非叶子结点索引/参数2:range的右范围,即到索引为0的第一个节点,右开特效所以为-1/参数3:步长,倒序为-1
# i代表建堆时调整的部分根的索引
sift(li, i, n-1) # i:根索引=指针low,n-1最后一个元素下标=high指针
# 建堆完成
for i in range(n-1, -1, -1):
# i指向当前堆的最后一个元素
li[0], li[i] = li[i], li[0]
sift(li, 0, i-1) # i-1是新的high
时间复杂度:O(nlogn)
python内置了import heapq堆模块,可以更简单的实现堆
堆排序应用:topk问题
现在有n个数,设计算法得到前k大的数。(k<n),类似场景:热搜榜前十
解决思路:
- 取列表前k个元素建立一个小根堆(堆顶数最小,从下到上,主键减小)。堆顶就是目前第k大的数。
- 依次向后遍历原列表,对于列表中的元素,如果小于堆顶,则忽略该元素;如果大于堆顶,则将堆顶更换为该元素,并且对堆进行调整;
- 遍历列表所有元素后,倒序弹出堆顶
def sift(li, low, high):
i = low # i最开始指向根节点
j = 2 * i + 1 # j开始指向左孩子
tmp = li[low] # 把堆顶保存起来,以便向下调整
while j <= high: # 只要j位置有数,即小于或等于最后一个元素
if j + 1 <= high and li[j + 1] < li[j]: # 如果有右孩子且右孩子<左孩子
j = j + 1 # j指向右孩子
if li[j] < tmp: # 比堆顶小
li[i] = li[j] # 新的堆顶为li[j]
# 往下看一层,i和j向下移一层
i = j # i向下移到j
j = 2 * i + 1 # j向下移到i的左孩子节点
else: # tmp更大,则把tmp放在i位置
li[i] = tmp # 把tmp放在某一个领导(非叶子结点)位置上
break
else:
li[i] = tmp # 如果j>high,把tmp放在叶子节点上
def topk(li,k):
heap = li[0:k]
for i in range((k-2)//2, -1, -1):
sift(heap, i, k-1)
# 1.建堆
for i in range(k, len(li)-1):
if li[i] > heap[0]:
heap[0] = li[i]
sift(heap, 0, k-1)
# 2.遍历
for i in range(k-1, -1, -1):
heap[0], heap[i] = heap[i], heap[0]
sift(heap, 0, i-1)
# 3.出数
return heap
li = list(range(100))
import random
random.shuffle(li)
print(li)
print(topk(li, 10))
归并排序
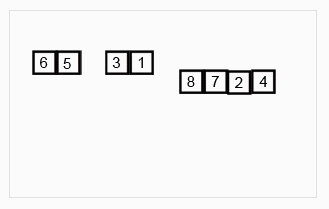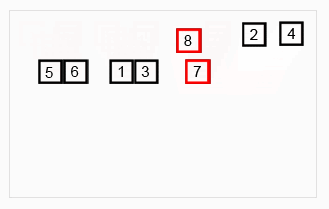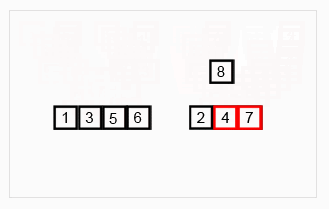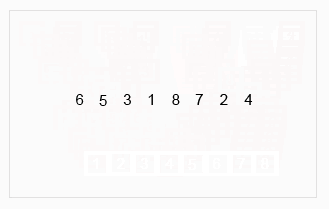
归并排序涉及到了递归
时间复杂度:O(nlogn)
空间复杂度:O(n)
python内部的sort基于归并排序
def merge(li, low, mid, high):
"""
归并的前提:列表分为两段有序
:param li:
:param low: 最左指针
:param mid: 随意的中间值的索引
:param high: 最右指针
:return:
"""
i = low
j = mid+1
ltmp = []
while i<=mid and j<=high: # 左右两边都有数
if li[i]<li[j]: # i指针小于j指针的数
ltmp.append(li[i]) # 把小的数加到新的列表中
i+=1
else:
ltmp.append(li[j])
j+=1
# while执行完,有一部分没值了
while i<=mid:
ltmp.append(li[i])
i+=1
while j <=high:
ltmp.append(li[j])
j += 1
li[low:high+1] = ltmp # 新建的列表写回原列表
def merge_sort(li, low, high):
"""
归并排序
:param li:
:param low: 最小值指针
:param high: 最大值指针
:return:
"""
if low<high: # 至少有两个元素,递归
mid = (low+high)//2 # mid经过递归,每次都在减半,直到减到1时,跳出进行归并
merge_sort(li, low, mid)
merge_sort(li, mid+1, high)
merge(li, low, mid, high)
NB三人组总结
1.时间复杂度都是O(nlogn)
2.速度:快速排序>归并排序>堆排序
3.缺点:
* 快速排序:极端情况下排序效率低(倒序)
* 归并排序:需要额外的内存开销(开辟一个新的列表ltmp)
* 堆排序:在NB三人组中,排序算法相对较慢
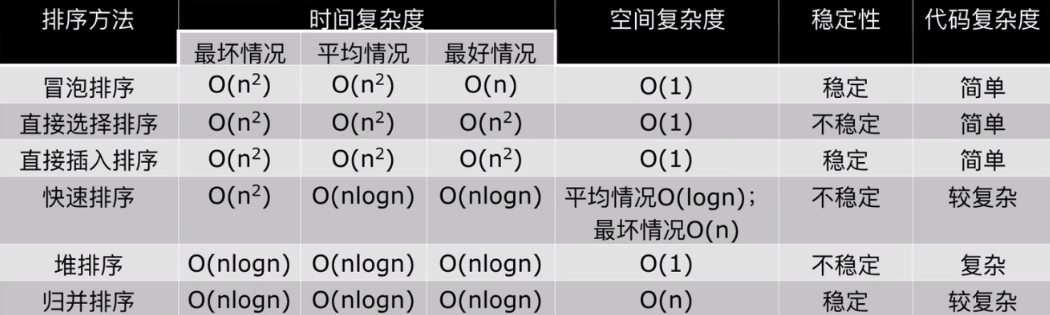
稳定性:
- 稳定排序:相同的元素进行排序,相同元素的原本位置前后顺序不会改变。在排序中前后交换位置都为稳定
- 不稳定排序:在排序中交换位置,飞着交换(跨过其他元素)都为不稳定