其他排序算法
希尔排序
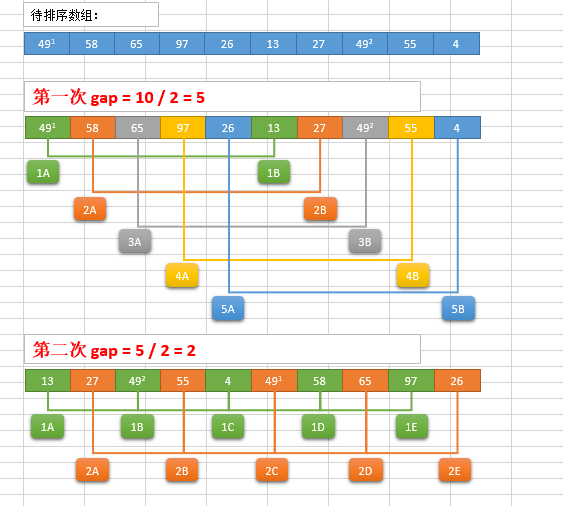
原理:希尔排序(Shell Sort)是一种分组插入排序算法(插入算法升级版)
希尔排序分析: 每次减半分为一组,gap=len(n)//2,每组再进行插入排序
def insert_sort_gap(li, gap):
for i in range(gap, len(li)): # i表示摸到的牌的下标
tmp = li[i]
j = i - gap # j指的是手里的牌的下标
while j >= 0 and li[j] > tmp:
li[j + gap] = li[j] # 摸到的牌和手上的牌的值进行替换
j -= gap # 这组的下一个值
li[j + gap] = tmp # 不进行交换,保留摸到的牌原本的值
def shell_sort(li):
d = len(li) // 2 # 进行分组
while d >= 1: # 分组结束条件为分组=1,
insert_sort_gap(li, d) # 调用插入排序
d //= 2 # 得到新的分组步长
时间复杂度:Shell复杂度与gap有关系,不同的gap导致不同结果
- 最优时间复杂度:根据步长序列的不同而不同
- 最坏时间复杂度:O(n2)
- 稳定想:不稳定
计数排序
速度快,使用需要有前提
def count_sort(li, max_count=100):
count = [0 for _ in range(max_count+1)]
print('func_count',count)
for val in li:
count[val] += 1 # 给对应位置计数+1
li.clear() # 清空原来列表,防止浪费空间复杂度
for ind,val in enumerate(count):
for i in range(val): # 循环每个元素的个数
li.append(ind) # 重新把数据写回原列表
import random
li = [random.randint(0,100) for _ in range(1000)]
print('first',li)
count_sort(li)
print('final',li)
时间复杂度:O(n),虽然有多个for循环,但是和n,即len(li)没有关系,只有第一个循环与n有关系,所以为O(n)
计数排序速度比任何排序都快,但是使用计数排序有前提:
必须知道列表的范围,数字大的也不行,因为如果只有五个数,每个数很大,则要开辟很大的空间
桶排序
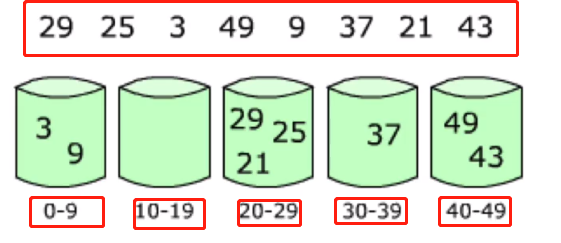
原理:计数排序中,如果元素范围比较大(例如:1~1亿之间)需要改造算法计数排序升级版,就是桶排序。首相将元素分在不同的桶中,再对每个桶中的元素排序
def bucket_sort(li, n=100, max_num=10000):
"""
桶排序
:param li: 列表
:param n: 桶的数目
:param max_num: 数的范围
:return:
"""
buckets = [[] for _ in range(n)] # 创建n个空桶[],每个桶可以放max_num//n个数的范围
for var in li:
i = min(var // (max_num//n),n-1) # i:var被放到几号桶
buckets[i].append(var) # 把var加到桶里
# 保持桶内的顺序
for j in range(len(buckets[i])-1,0,-1): # 倒过来进行桶内排序
if buckets[i][j]< buckets[i][j-1]: # 与新加进来的数进行比较
buckets[i][j], buckets[i][j-1] = buckets[i][j-1],buckets[i][j]
else:
break
sorted_li = []
for buc in buckets:
sorted_li.extend(buc)
return sorted_li
import random
li = [random.randint(0, 100) for i in range(10000)]
li = bucket_sort(li)
print(li)
桶排序的表现取决于数据的分布。也就是需要对不同的数据排序时使用不同的分桶策略
时间复杂度:
- 平均情况:O(n+k)
- 最坏情况:O(n^2k)
- 空间复杂度:O(nk)
基数排序
本质:多关键字排序
根据数字不同位数,分成n个桶
桶排序的升级版本
def radix_sort(li):
max_num = max(li) # 最大值9->1, 99->2, 888->3, 10000->5
it = 0
while 10 ** it <=max_num:
buckets = [[] for _ in range(10)]
for var in li:
# 987 it=1 987//10->98 98%10->8; it=2 987//100->9 9%10=9
digit = (var//10**it)%10
buckets[digit].append(var)
# 分桶完成
li.clear()
for buc in buckets:
li.extend(buc)
# 把数重新写回li
it += 1
时间复杂度:O(kn)
空间复杂度:O(k+n)
k表示数字位数