数据结构
数据结构按照逻辑结构可分成3种
1.线性结构:数据结构中元素存在一对一的相互关系
2.树结构:数据结构中元素存在一对多的相互关系
3.图结构:数据结构中元素存在多对多的相互关系
列表
32位机器上,一个整数占4个字节,一个地址占4个字节
64位则8个字节
数组和列表有两点不同:
1.数组元素类型要相同,列表元素可以为多种类型的元素
2.数组的长度固定
python列表不是存真实值,而是存内存地址
顺序表的实现方式(数组/列表):
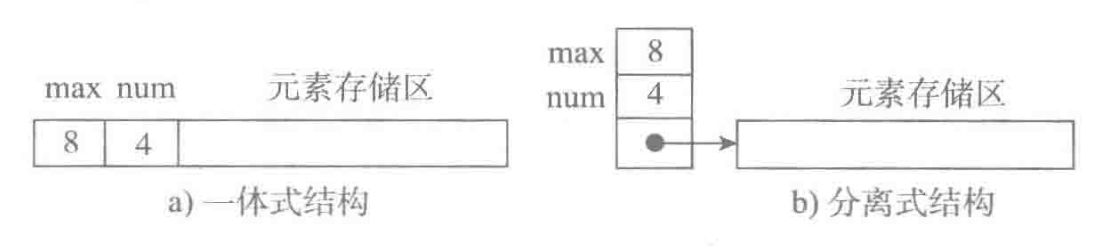
图a为一体式结构(数组),存储表信息的单元与元素存储区以连续的方式安排在一块存储区里,两部分数据的整体形成一个完整的顺序表对象。
一体式结构整体性强,易于管理。但是由于数据元素存储区域是表对象的一部分,顺序表创建后,元素存储区就固定了。
图b为分离式结构(列表),表对象里只保存与整个表有关的信息(即容量和元素个数),实际数据元素存放在另一个独立的元素存储区里,通过链接与基本表对象关联。
*
**元素存储区替换:
一体式结构由于顺序表信息区与数据区连续存储在一起,所以若想更换数据区,则只能整体搬迁,即整个顺序表对象(指存储顺序表的结构信息的区域)改变了。
分离式结构若想更换数据区,只需将表信息区中的数据区链接地址更新即可,而该顺序表对象不变。
扩充的两种策略:
1.每次扩充增加固定数目的存储位置,如每次扩充增加10个元素位置,这种策略可称为线性增长。
特点:节省空间,但是扩充操作频繁,操作次数多。
2.每次扩充容量加倍,如每次扩充增加一倍存储空间。
特点:减少了扩充操作的执行次数,但可能会浪费空间资源。以空间换时间,推荐的方式。
*
**python中list/tuple采用了顺序表。其中tuple是不可变类型;list就是一种采用分离式技术实现的动态顺序表
list内置操作的时间复杂度:

栈
栈(Stack)是一个数据结合,只能在一端进行插入或删除操作的列表
特点:后进先出(last-in,first-out)
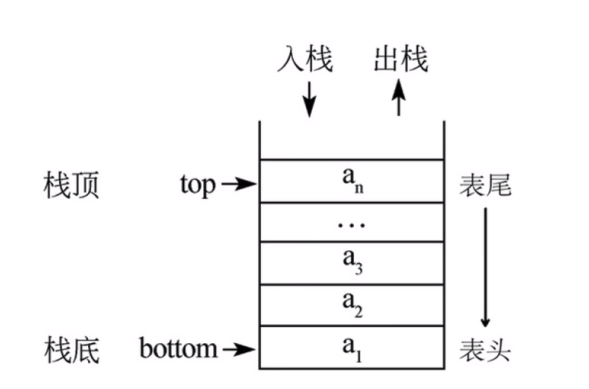
栈的基本操作:
1.进栈(压栈):push li.append
2.出栈:pop li.pop
3.取栈顶:gettop li[-1]
class Stack(object):
"""栈"""
def __init__(self):
self.stack = []
def is_empty(self):
"""判断是否为空"""
return self.stack == []
def push(self, stack):
"""加入元素"""
self.stack.append(stack)
def pop(self):
"""弹出元素"""
return self.stack.pop()
def get_top(self):
"""返回栈顶元素"""
if len(self.stack) > 0:
return self.stack[len(self.stack) - 1]
return None
def size(self):
"""返回栈的大小"""
return len(self.stack)
if __name__ == "__main__":
stack = Stack()
stack.push("hello")
stack.push("world")
stack.push("itcast")
print(stack.size())
print(stack.get_top())
print(stack.pop())
print(stack.pop())
print(stack.pop())
栈的应用:括号匹配问题
def brace_match(s):
match = {')': '(', ']': '[', '}': '{'}
stack = Stack() # 调用栈
for ch in s:
if ch in {'(', '[', '{'}:
stack.push(ch)
else: # ch in {')',']','}'}
if stack.is_empty():
return False
elif stack.get_top() == match[ch]:
stack.pop()
else:
return False
if stack.is_empty():
return True
else:
return False
print(brace_match('[{()}()]{[]}'))
队列
仅允许在列表的一端进行插入,另一端进行删除
性质:先进先出
队头:front/队尾:rear
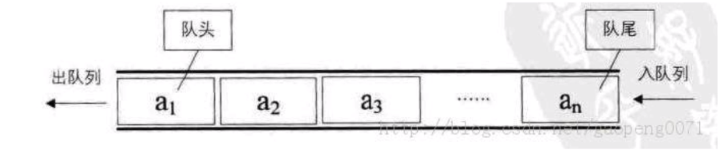
环形队列:
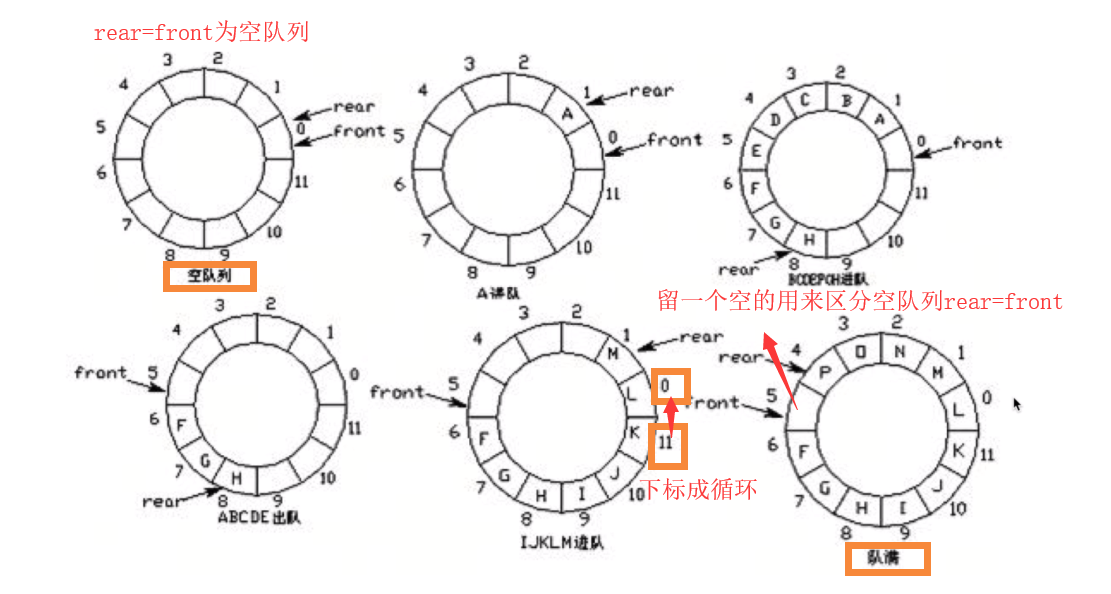

class Queue():
def __init__(self, size=100):
self.queue = [0 for _ in range(size)]
self.size = size
self.rear = 0 # 队尾指针
self.front = 0 # 队首指针
def push(self, element):
if not self.is_filled():
self.rear = (self.rear + 1) % self.size
self.queue[self.rear] = element
else:
raise IndexError("Queue is filled")
def pop(self):
if not self.is_empty():
self.front = (self.front + 1) % self.size
return self.queue[self.front]
else:
raise IndexError('Queue is empty')
def is_empty(self):
"""
判断队空
:return:
"""
return self.rear == self.front
def is_filled(self):
"""
判断队满
:return:
"""
return (self.rear + 1) % self.size == self.front
q =Queue(5)
for i in range(4):
q.push(i)
print(q.is_filled()) # 满了
print(q.pop())
print(q.pop())
双向队列(dequeue):
两端都可以支持进队和出队的操作
from collections import deque
q = deque([1,2,3],2)
print(q) # deque([2, 3], maxlen=2)
q.append(6) # 队尾进队,把2挤掉,3变为队首
print(q.popleft()) # 队首出队:3
# 用于双向队列
q.appendleft(1) # 队首进队
print(q) # deque([1, 6], maxlen=2)
q.pop() # 队尾出队
print(q) # deque([1], maxlen=2)
应用: 读取文件后n行
def tail(n):
"""
读取文件后n行
:param n: 行数
:return:
"""
with open('test.txt', 'r') as f:
q = deque(f, n)
return q
for line in tail(5):
print(line, end='')
栈和队列的应用:迷宫问题

栈—–深度优先搜索:
回溯法
思路:
从一个节点开始,任意找下一个能走的点,当找不到能走的点时,退回上一个点寻找是否有其他方向的点。
使用栈存储当前路径
maze = [
[1, 1, 1, 1, 1, 1],
[1, 0, 0, 1, 0, 1],
[1, 0, 1, 0, 0, 1],
[1, 0, 1, 0, 1, 1],
[1, 0, 1, 0, 0, 1],
[1, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1]
]
dirs = [
lambda x, y: (x + 1, y), # 向上走,x往上移一层
lambda x, y: (x - 1, y), # 向下走
lambda x, y: (x, y - 1), # 向左
lambda x, y: (x, y + 1), # 向右
]
def maze_path(x1, x2, y1, y2):
"""
解决迷宫问题
:param x1: 起始x
:param x2: 起始y
:param y1: 终点x
:param y2: 终点y
:return:
"""
stack = [] # 存放走过的坐标
stack.append((x1, y1))
while len(stack) > 0: # 有坐标能走
curNode = stack[-1] # 当前节点
if curNode[0] == x2 and curNode[1] == y2:
# 走到终点了
for p in stack:
print(p)
return True
# x,y四个方向 x+1,y /x-1,y /x,y-1 /x,y+1
for dir in dirs:
nextNode = dir(curNode[0], curNode[1]) # 拿到当前能走的坐标
# 如果下一个节点能走
if maze[nextNode[0]][nextNode[1]] == 0:
stack.append(nextNode)
maze[nextNode[0]][nextNode[1]] = 2 # 2表示已经走过的坐标
break
# 如果maze[nextNode[0]][nextNode[1]] == 其他值,则直接进入下一循环
else:
maze[nextNode[0]][nextNode[1]] = 2
stack.pop()
else:
print("没有路了")
return False
maze_path(1, 1, 1, 4)
队列—–广度优先搜索:
思路:
从一个节点开始,寻找所有接下来能继续走的点,继续不断寻找,直到找到出口。
使用队列存储当前正在考虑的节点
队列能找到最短路径,能够同时走多条路径
from collections import deque
maze = [
[1, 1, 1, 1, 1, 1],
[1, 0, 0, 1, 0, 1],
[1, 0, 1, 0, 0, 1],
[1, 0, 1, 0, 1, 1],
[1, 0, 1, 0, 0, 1],
[1, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1]
]
dirs = [
lambda x, y: (x + 1, y), # 向上走,x往上移一层
lambda x, y: (x - 1, y), # 向下走
lambda x, y: (x, y - 1), # 向左
lambda x, y: (x, y + 1), # 向右
]
def print_r(path):
"""
打印走到终点的路径
:param path:
:return:
"""
real_path = [] # 真实路径
i = len(path) - 1 # 最后一个坐标下标
while i >= 0: # 路径里还有值,从终点往前推
real_path.append(path[i][0:2]) # 添加当前最后一个坐标x,y和上一个路径的下标
# print(real_path)
i = path[i][2] # 拿到上一个路径的下标
real_path.reverse() # 路径翻转,从起点走
for node in real_path:
print(node)
def maze_path_queue(x1, x2, y1, y2):
"""
解决迷宫问题
:param x1: 起始x
:param x2: 起始y
:param y1: 终点x
:param y2: 终点y
:return:
"""
queue = deque()
path = [] # 存储下标,即每个坐标上一个位置的由来,其中第一个数没有由来,自定义为-1
queue.append((x1, y1, -1)) # 从右边进来,坐标定义为-1
while len(queue) > 0: # 队列不空循环
cur_node = queue.popleft() # 从左边出去
path.append(cur_node)
if cur_node[0] == x2 and cur_node[1] == y2:
# 到达终点
print_r(path)
return True
for dir in dirs: # 有几个方向,就同时走几个方向
next_node = dir(cur_node[0], cur_node[1])
if maze[next_node[0]][next_node[1]] == 0:
queue.append((next_node[0], next_node[1], len(path) - 1))
maze[next_node[0]][next_node[1]] = 2 # 标记为已走过
return False
maze_path_queue(1, 1, 1, 4)